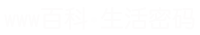吴国平：毫不起眼的√2，为何能让东西方文明走上不同的发展轨迹？

2026-01-11

提示您，本文原题为 -- 吴国平：毫不起眼的√2 ，为何能让东西方文明走上不同的发展轨迹？

在一条数轴上，既有无理数，也存在着有理数，这些数相互“紧挨”着凑在一起，构成了实数。

说到实数，相信大家都非常熟悉，它应该也是日常生活中用到的最多数学知识内容之一。不过，在几千年前的人类社会，当时的数学界并没有真正认识到无理数的存在，数学的研究和发展基本上只停留在有理数的范围之内，解决问题一般用整数和分数来进行计算。

那么无理数是如何出现在数学这个大家庭当中呢？

吴国平：毫不起眼的√2 ，为何能让东西方文明走上不同的发展轨迹？// //

?说到无理数的出现，就不得不提一个人，那就是毕达哥拉斯。

毕达哥拉斯是古希腊时期著名的数学家、哲学家，他和他的毕达哥拉斯学派是最早把数的概念提到突出地位的学术流派。毕达哥拉斯对数学的痴迷，可以说是达到了狂热的程度，他认为人类生活的世界，可以用“数”来解释一切，认为“数”是这个世界万物的本原。

毕达哥拉斯认为宇宙的一切事物的度量都可用整数或整数的比来表示，除此之外，就再没有其他了。

如一个苹果的“一”可以用数“1”来表示，两个人的“两”也可以用数“2”来表示，这让人们相信“数”是构成现实世界的基础，基于这样的简单逻辑关系，毕达哥拉斯学派认为数学存在的意义，并不是为了计算、证明、推理等，而是可以帮助人类探索大自然的奥秘。

吴国平：毫不起眼的√2 ，为何能让东西方文明走上不同的发展轨迹？// //

?

毕达哥拉斯学派把数学和生活之间进行联系，得出一些逻辑关系，这些逻辑关系在今天看来属于比较简单和低层次，但在几千年前的人类社会，确实是非常大的进步，给当时哲学和数学的发展，带来巨大的影响。

因此，毕达哥拉斯学派就此提出了“万物皆数”、“数是万物的本质”、“存在由之构成的原则”等抽象和夸大的数为宇宙本原的理论，将“数”神秘化，认为“数”是众神之母，它是普遍的始原，是自然界中对立性和否定性的原则，试图建立起整个宇宙是“数”及其关系的和谐的体系。

俗话说物极必反，当毕达哥拉斯在神话“数”的路上越走越远的时候，他学派当中的一名学生希帕索斯发现一个不可理解的问题：边长为1的正方形其对角线长度是多少呢？或是认为等腰直角三角形的直角边与其斜边是不可通约的。

吴国平：毫不起眼的√2 ，为何能让东西方文明走上不同的发展轨迹？// //

?

希帕索斯善于观察、分析和思考，他经过大量的计算和研究，发现这一对角线的长度既不能用整数表示，也不能用分数来表示，并不存在于已知的数当中，也就是说“它”是未知的。

希帕索斯把这一未知的数告诉了毕达哥拉斯本人以及学派的其他成员，却引起了大家的恐慌。

因为毕达哥拉斯学派一直认为“万物皆数(指整数)” ，数学的知识是可靠的、准确的，而且可以应用于现实的世界，数学的知识由于纯粹的思维而获得，不需要观察、直觉和日常经验。

毕达哥拉斯学派一直认为任何量，在任何精确度的范围内都可以表示成有理数，这在当时的西方数学界属于至高无上的信仰和权威。现在出现一个未知的数，却显得那么“无理” ，无法用整数和分数来表示，这自然就与整个毕达哥拉斯学派学内部形成了对立。

吴国平：毫不起眼的√2 ，为何能让东西方文明走上不同的发展轨迹？// //

?

因此，毕达哥拉斯学派所建立起的“万物皆数(指整数)”的理论，却被希帕索斯发现的“未知数”给无情推翻了，更糟糕的是面对这一恐慌，毕达哥拉斯学派却毫无解决办法。

毕达哥拉斯学派为了掩盖这一“无理数”的存在，就把被希帕索斯投进了大海，处以“淹死”的惩罚。

边长为1的正方形其对角线长度等于√2 ，这样简单的计算题很多人都会，也很容易理解。不过，在当时的数学界，却引起极大的恐慌，掀起了一场巨大风暴。

√2的出现直接动摇了毕达哥拉斯学派的数学信仰，对毕达哥拉斯学派和西方数学界带来了致命打击，导致人类历史第一次数学危机的发生。

第一次数学危机是数学史上的一次重要事件，以√2的发现为导火线，最终以无理数的定义出现为结束标志。

吴国平：毫不起眼的√2 ，为何能让东西方文明走上不同的发展轨迹？// //

?

第一次数学危机的出现和解决，改变了一直以来在西方数学界占据主导地位的毕达哥拉斯学派，同时标志着西方世界关于无理数研究的开始。

第一次数学危机的顺利解决，给当时的西方数学界带来极大的影响，特别是对古希腊人来说，这些影响更加深远，如整数的崇高地位受到挑战和质疑，人们也开始认识到几何学的某些真理与算术无关，一些几何量也并不能完全由整数及其比来表示，而数却可以由几何量表示出来。也认识到直觉和经验不一定靠得住，而推理证明才是准确可靠的。

从此，几何学开始在希腊数学中占有特殊地位，古希腊人从一个极端走向另一个极端。如希腊人开始从“自明的”公理出发，经过演绎推理，并由此建立几何学体系，这也算是第一次数学危机的自然产物，给数学发展带来进步。

吴国平：毫不起眼的√2 ，为何能让东西方文明走上不同的发展轨迹？// //

?

不过，对于其他古文明来说，就没有这么幸运，如对于古代中国、古埃及、巴比伦、古印度等国的数学发展来说，并没有经历类似的数学危机，继续走着以“算术”和实用为主的发展道路。

如据史籍记载，虽然在古代中国就很早发现了无理数，但古代中国数学家却满足于实际应用的数的运算，从开方不尽的计算过程入手，通过计算方式来认识并建立其法则。

第一次数学危机的发生和解决，完全改变了东方世界和西方世界的数学发展，希腊人开始研究几何量的长度关系，从线段不可公度的几何角度入手，用逻辑方法进行探讨，形成了欧几里得《原本》的公理体系与亚里士多德的逻辑体系，为世界数学发展作出了另一种杰出的贡献。

不过，虽然古希腊人经过第一次数学危机走上了不同的数学发展道路，但又是走向了另一个极端，从“数”走向“形” ，这让古希腊人把几何看成了全部数学的基础，把数的研究隶属于形的研究，人为的分割了数与形之间的紧密联系。这种极端化发展形式，最大的恶果就是古希腊数学家完全抛弃了无理数，直接限制了算术和代数的发展，造成相关基本理论非常欠缺，而这样的极端发展形式，整整影响了欧洲两千多年的数学发展。

推荐阅读

上一篇：中华史诗美术大展丨146幅全国名家力作欣赏(油画组)

下一篇：张学良《西安事变反省录》再研究